 |
Nous allons nous intéresser au comportement dynamique des suspensions.
Comment réagissent ces suspensions en virage et en freinage? C'est à cette question que nous allons essayer de répondre.
Le cas du virage
Prenons une voiture équipée d'une suspension MacPherson. Nous allons supposer que la voiture prend un virage vers la droite, les roues de droite sont en limite de décollement, m est la masse équivalente sur le train avant (environ deux tiers de la masse totale du véhicule), regardons ce qui se passe au niveau du train avant.
Nous ferons les hypothèses suivantes:
- Le problème est considéré comme plan.
- Tous les éléments seront considérés comme rigides, y compris les ensembles ressort+amortisseur (leurs ecrasements seront negligés dans cette première phase d'étude).
- Les contacts roues/sol seront assimilés a des liaisons ponctuelles.
- L'action de l'air (frottement) ne sera pas prise en compte.
- G est le centre de masse de l'ensemble véhicule+pilote de masse totale M.
Paramétrons le problème: | 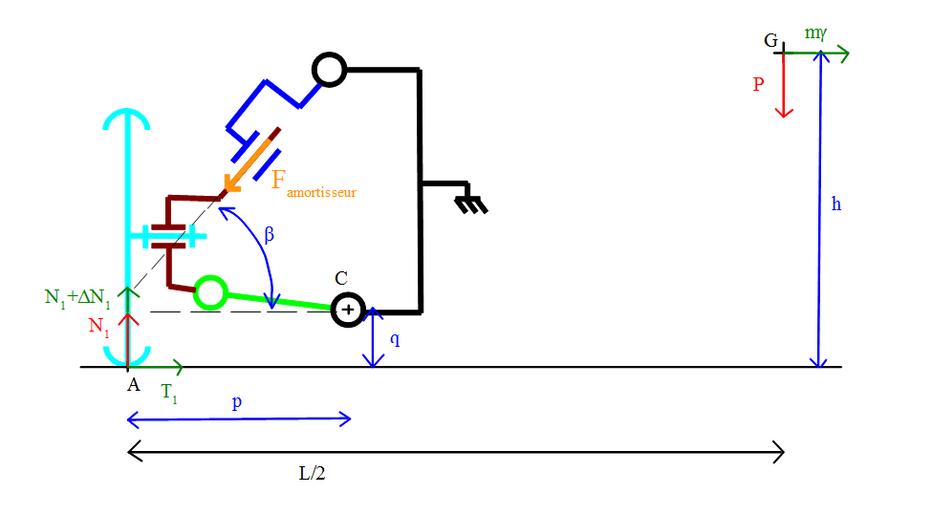 |
|
Le problème est symétrique en statique, on a une réaction N2 au point B (le point de contact entre la roue droite et le sol).
On applique d'abord le Principe Fondamental de la Statique au véhicule, au point A:
| 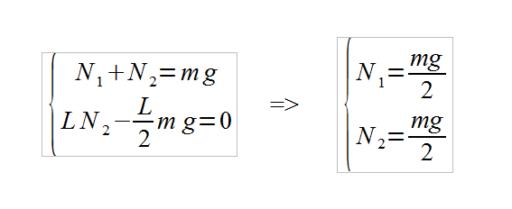 |
|
| Puis on applique le PFD au véhicule en A, on suppose qu'il y a limite de décollement sur la roue droite: | 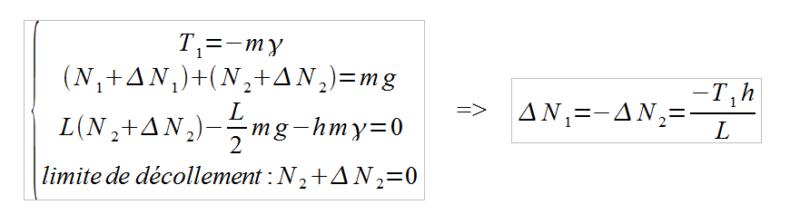 |
|
On peut ainsi trouver la valeur de l'effort additionnel dans la suspension en virage.
Si maintenant on isole l'ensemble triangle+porte-moyeu+roue, le théorème du moment dynamique donne: | 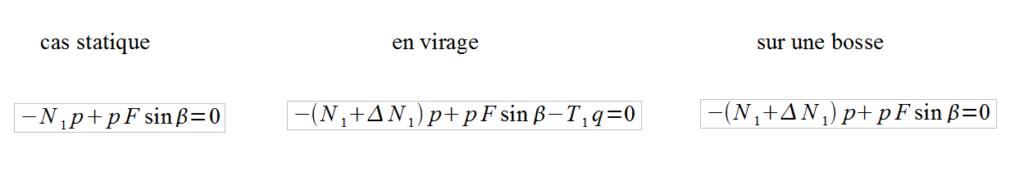 |
|
| On peut alors donner une définition du coefficient anti-roulis: | 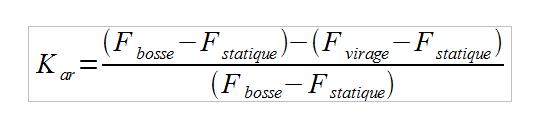 |
|
| On a donc: | 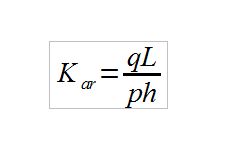 |
|
Cette définition se traduit par:
Kar=1 => Correction anti-roulis totale, pour un même effort dans la suspension en virage que sur une bosse, on n'a aucun roulis en virage.
Kar=0 => Pas de correction anti-roulis, la suspension voit le même enfoncement dans le cas du virage et dans le cas d'une bosse.
Kar<0 => La voiture prend plus de roulis en virage que sur une bosse.
Kar>1 => La voiture ressent un roulis inversé en virage. | |
|
Ceci est intéressant dans le cas de la suspension MacPherson, mais qu'en est-il des autres types de suspension?
Dans le cas général, il se trouve que le point C est le centre instantanné de rotation de la suspension, pour les autres types de suspensions, il suffit de trouver le centre instantanné de rotation Cir pour appliquer les mêmes calculs. Par exemple, voici le Cir d'une suspension double triangle: | 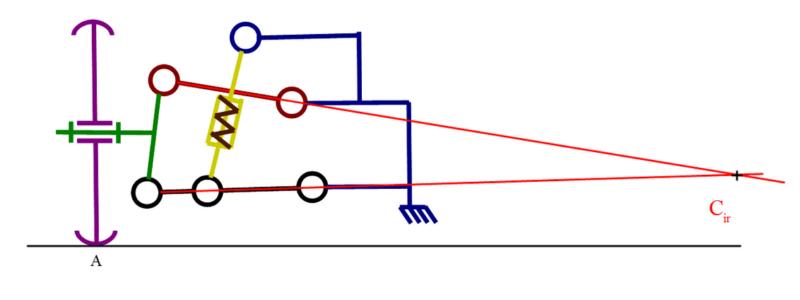 |
|
| En effet, une seule barre de liaison articulée comme ci-dessous est totalement équivalente du point de vue cinématique à l'ensemble roue-moyeu, triangle supérieur et triangle inférieur. | 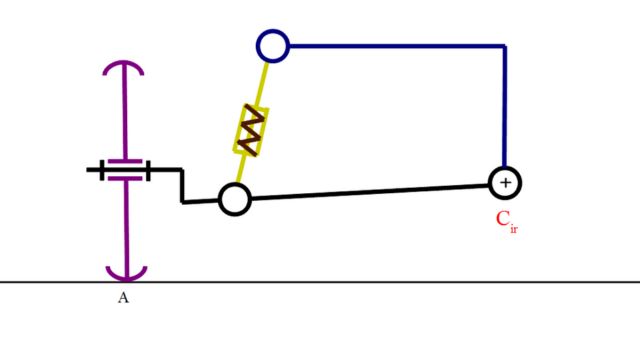 |
|
C'est pour cela qu'on peut appliquer les mêmes calculs dès qu'on a le centre instantanné de rotation.
Le cas du freinage
Dans le cas du freinage, nous avons le même type de calculs avec le paramétrage suivant (L est la distance de la roue avant à la roue arrière): | 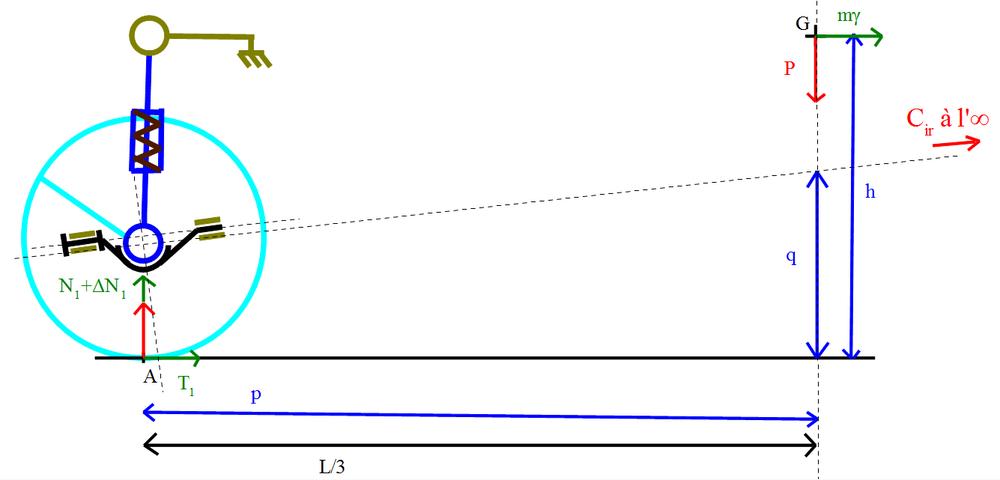 |
|
On retrouve ainsi les mêmes calculs.
On peut définir le coefficient anti-plongée, avec le second paramétrage: | 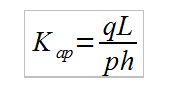 |
|
| Exemple de Cir en freinage pour une suspension double triangle: | 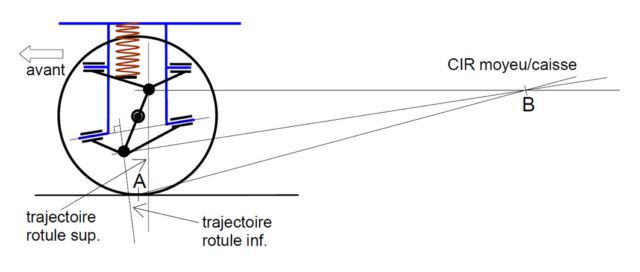 |
|
| C'est avec les études dynamiques réalisées qu'on peut déterminer tous les efforts dans les rotules et paliers des suspensions, c'est ce qui permet de choisir et dimensionner les liaisons entre les différentes pièces. |
|







